Pipetlerin kalibre edilmesi hakkındaki yayınımızdan (bu linkten yayına ulaşabilirsiniz) aşağıdaki formülleri formülleri hatırlayacaksınız.
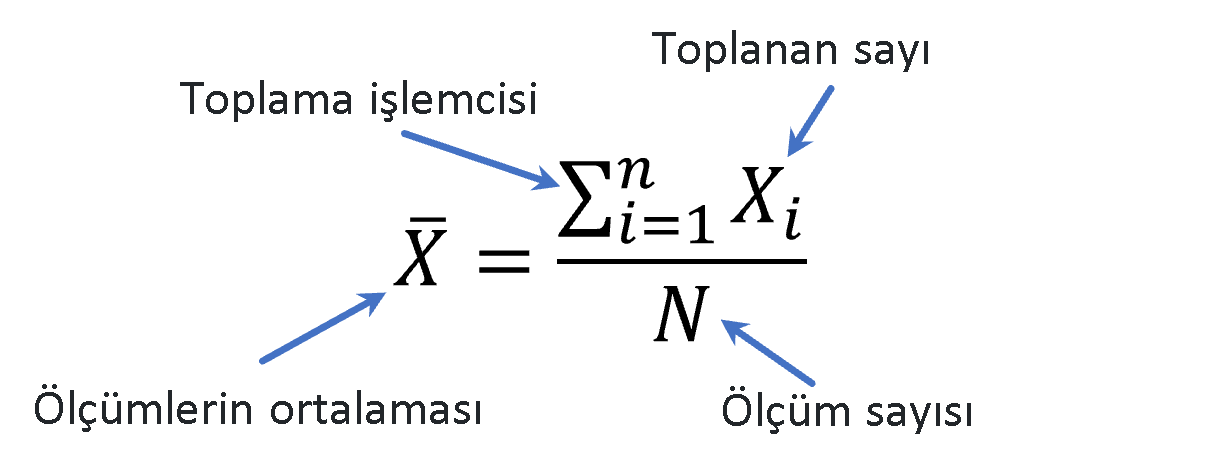
Ölçümlerin ortalama değerinin bulunduğu formülü açıklayacak olursak;
Deneyde 5 ölçüm yapılmıştır. Bu ölçümleri X ile gösterirsek, i indiside ölçüm sırasını ifade eder ve 1. ölçüm için Xi=X1, 2. ölçüm X2, ... ve 5. ölçüm X5 olarak ifade edilir. Formüldeki
Standart sapmanın bulunduğu formülü ise 3 aşamada inceleyelim.
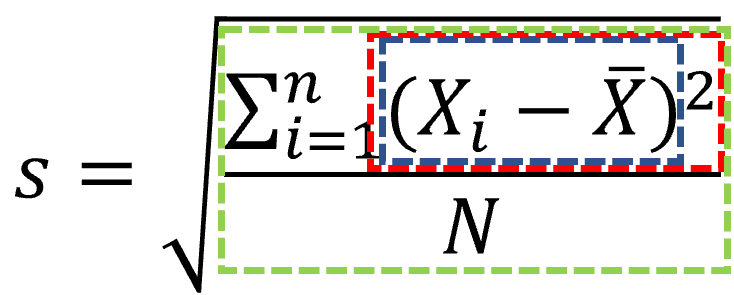
Formüldeki mavi dikdörtgen içerisindeki kısım her bir ölçüm değerinin (X1, X2, ..., X5) sırasıyla ortalama değerden (X̄) çıkarılmasını ifade eder. Kırmızı dikdörtgende ise her bir çıkarma işleminin karesinin alınması gerektiğini gösterir. Yeşil dikdörtgen ise her bir çıkarma işleminin karesinin toplamının ölçüm sayısına bölünmesi gerektiğini ifade eder. Formülden de görüldüğü gibi en son olarak sonucun karekökünün alınmasıyla standart sapma hesaplanmış olur. Ölçüm sonuçlarından elde edilen değerleri kullanarak ortalama ve standart sapmayı hesaplayıp tablolaştıralım.
Çalışılan sıcaklık için Z-faktörü tablodan 1,0025 olarak elde edilir. Z-faktörü ile kütle ölçümü değeri çarpıldığında ise karşılık gelen hacim değerleri elde edilmiş olur. Burada dikkat ederseniz g değerleri 1000 ile çarpılarak miligram'a çevrilir ve Z-faktörü ile çarpılarak karşılık gelen μl biriminde hacim elde edilir.
| Ölçüm | Terazide okunan değer (g) | Karşılık gelen hacim (μl) |
| 1 | 0,1915 | 191.98 |
| 2 | 0,1922 | 192.68 |
| 3 | 0,1973 | 197.79 |
| 4 | 0,1976 | 198.09 |
| 5 | 0,1946 | 195.09 |
Bu 5 değerin ortalama sonucu ise bize ölçülen hacim değerlerinin ortalamasını verecektir.
Ortalama değeri bulduktan sonra standart sapmayı hesaplayalım. Bunu ise bir tablo şeklinde ifade edelim.
| Ölçüm | (X-X̄) | (X-X̄)2 | Σ(X-X̄)2 |
| 1 | -3.14785 | 9.908959623 | 31.810458 |
| 2 | -2.4461 | 5.98340521 | |
| 3 | 2.66665 | 7.111022223 | |
| 4 | 2.9674 | 8.80546276 | |
| 5 | -0.0401 | 0.00160801 |
Standart sapmayı bulmak için ise Σ(x-x̄)2 değerini serbestlk derecesine (N-1, bu örnek için 4) bölüp karekökünü almak gerekir. Bu örnek için s=2,82 olarak hesaplanmış olur.
Ölçüm belirsizliği ise aşağıdaki formüle göre
olarak hesaplanır. Son olarak doğruluk
olarak dolayısıyla hata ise %2,44 olarak bulunur. Hatırlayacağınız gibi pipet ile verilen spesifikasyonlar kontrol edilerek pipet uygunluğu kontrol edilir.
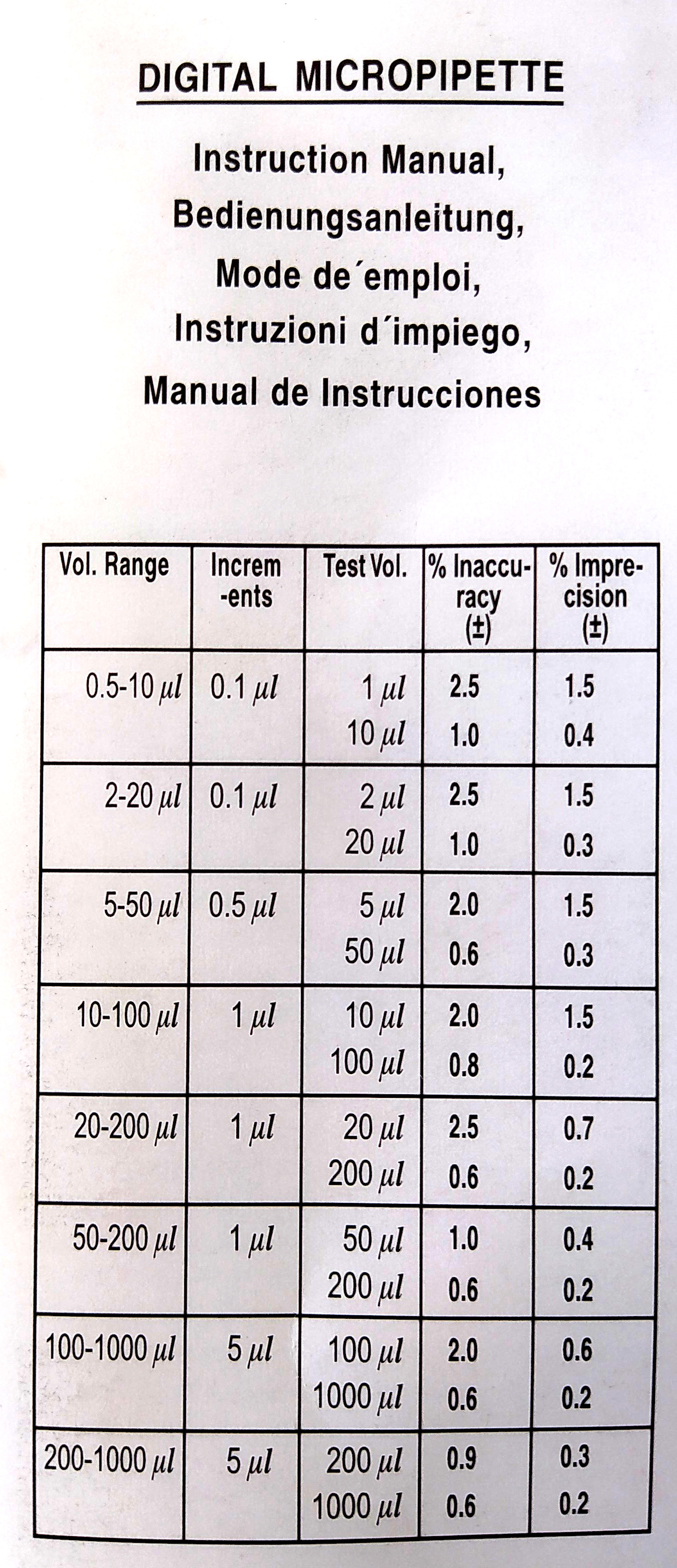 |
200 μl için hata (%Inaccuracy) yüzde ±0,6 ve belirsizlik (%Imprecision) ±0,2 değerinden büyük olamaz. Dolayısıyla bu pipet ile 200 μl hacim için yapılan ölçümler yüksek hata içerir ve uygun değildir. Pipet bakımları yapılarak ayarlanmalı ve yeniden kalibre edilmelidir. |
